Master Thesis (2005)
In my last year of college at KULeuven, I chose to make my master thesis in the computer graphics group. I extended an existing algorithm to convert a 3D polygon model to a surfel representation. My promotor was prof. dr. ir. Philip Dutré and my mentor Bart Adams.
Polygons vs Surfels
Polygons define a 3D model by a number of connected faces, where each face is a closed shape bounded by three or more line segments. Surfels (short for SURFace ELementS) on the other hand are a representation consisting of a number of discs that are not connected. Each disc is represented by a 3D point (its center), a radius (two in case of an ellips), a normal and a color.
The Algorithm
Describing the entire algorithm would take far too long, so I'll briefly describe each step. First, a large set of point samples is taken from the polygon model. This can be done in several ways and the exact way in which this is done determines how good the rest of the algorithm will perform, especially if textures are introduced. Secondly, the set is simplified to a small(er) set of surfels. This is done by growing selected samples to circular (or elliptical) discs and removing the point samples that lie 'close' beneath those discs. Of course an optimal selection has to be found that allows no holes in the surface mesh, but where the amount of overlap is minimal.
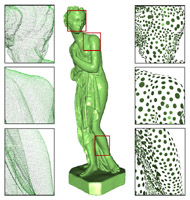
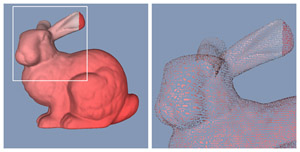
The left image shows both the polygon and surfel representation of the famous bunny model, the right image shows a set of point samples and its resulting simplification.
Left image from Bart Adams (I adjusted the colors).
Right image from 'Optimized Sub-Sampling of Point Sets for Surface Splatting' by Jainhua Wu, Leif Kobbelt.
Extension
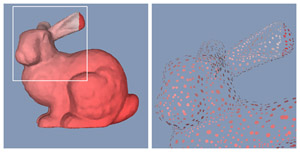
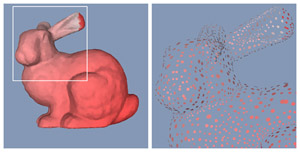
The goal of my master thesis was to extend the previous algorithm so it would take color into account. This way a textured model could also be converted to a corresponding surfel representation. The biggest change to the algorithm is the generation of the surfels from the set of point samples. A surfel can now not only cover samples that lie close to it, but the covered point samples must also have similar colors to be replaced by the surfel.
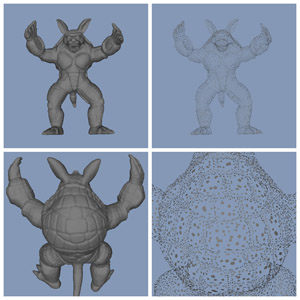
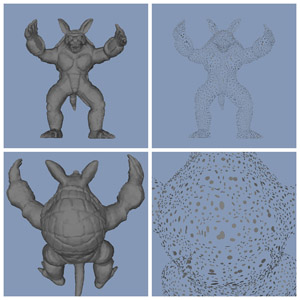
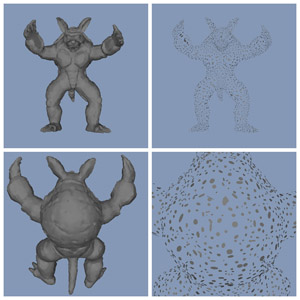
Results
Conclusion
The algorithm was written in C++ and performed best for organic models where certain error-tolerance variables enabled me to balance between detail and surfel reduction. A number of extensions are possible, such as truncated surfels. But to be honest ... I now understand why polygons are (and very likely will remain) the most-used representation form for 3D models.